Chapter 9 Standard MNL

Sources for this chapter:

Data for this chapter:

  • The bfast data is used from the MKT4320BGSU course package. Load the package and use the data() function to load the data.

    # Load the course package
library(MKT4320BGSU)
# Load the data
data(bfast)

9.1 Introduction

Base R is not good for standard multinomial logistic regression (MNL). The best package that I have found for standard MNL is nnet with its multinom function. Install that package install.packages("nnet") and load it.

library(nnet)

In addition, I have created some user defined functions, which are all in the MKT4320BGSU package.

  • stmnl produces Odds Ratio coefficients table, overall model significance, and McFadden’s Pseudo-\(R^2\)
  • stmnl_cm1 produces a Classification Matrix
  • stmnl_pp produces average predicted probability tables and plots

9.2 Data Preparation

As with binary logistic regression, we often us a training and holdout sample when using MNL. For standard MNL, the process is the same.

library(caret)
set.seed(4320)
inTrain <- createDataPartition(y=bfast$bfast, p=.75, list=FALSE)
train <- bfast[inTrain,]
test <- bfast[-inTrain,]

9.3 Standard MNL using multinom()

  • Standard MNL is performed using the multinom() function from the nnet package
  • Usage: multinom(formula, data)
    • formula is represented by dependent variables on the left side separated from the independent variables on the right side by a tilde(~), such as: dv ~ iv1 + iv2
    • data is the name of the (usually) training data
  • As with other analyses, we save the result of the model to an object
    • summary() provides standard coefficient estimates (i.e., not Odds Ratio estiamtes), but does not provide overall model fit values (i.e., overall model \(p\)-value or McFadden’s Psuedo \(R^2\)) or p-values for each independent variable
library(nnet)
model <- multinom(bfast ~ gender + marital + lifestyle + age, data=train)
# weights:  18 (10 variable)
initial  value 727.281335 
iter  10 value 579.014122
final  value 574.997631 
converged
summary(model)
Call:
multinom(formula = bfast ~ gender + marital + lifestyle + age, 
    data = train)

Coefficients:
        (Intercept)  genderMale maritalUnmarried lifestyleInactive         age
Bar       0.8832457 -0.21298963        0.6126977        -0.7865772 -0.02532866
Oatmeal  -4.4920408 -0.02262325       -0.3897362         0.3187473  0.07996475

Std. Errors:
        (Intercept) genderMale maritalUnmarried lifestyleInactive         age
Bar       0.3256994  0.2064320        0.2123832         0.2090460 0.006655803
Oatmeal   0.4596750  0.2094666        0.2366511         0.2156992 0.007755708

Residual Deviance: 1149.995 
AIC: 1169.995

9.3.1 stmnl() User Defined Function

  • To get overall model fit values, as well as an Odds Ratio estimate table with p-values, the stmnl() user defined function can be used
  • Usage: stmnl(model)
    • model is the name of the object with the saved model results
  • NOTE: This function requires the broom package. If you do not have it installed on your machine, you will need to install it.
stmnl(model)
LR chi2 (8) = 288.1568; p < 0.0001
McFadden's Pseudo R-square = 0.2004

 y.level              term estimate std.error statistic p.value
     Bar       (Intercept)   2.4187    0.3257    2.7118  0.0067
     Bar        genderMale   0.8082    0.2064   -1.0318  0.3022
     Bar  maritalUnmarried   1.8454    0.2124    2.8849  0.0039
     Bar lifestyleInactive   0.4554    0.2090   -3.7627  0.0002
     Bar               age   0.9750    0.0067   -3.8055  0.0001
 Oatmeal       (Intercept)   0.0112    0.4597   -9.7722  0.0000
 Oatmeal        genderMale   0.9776    0.2095   -0.1080  0.9140
 Oatmeal  maritalUnmarried   0.6772    0.2367   -1.6469  0.0996
 Oatmeal lifestyleInactive   1.3754    0.2157    1.4777  0.1395
 Oatmeal               age   1.0832    0.0078   10.3104  0.0000

9.3.2 Classification Matrix

  • To get a classification matrix, the stmnl_cm user-defined function should be used
  • Usage: stmnl_cm(model, data)
    • model is the name of the object with the saved model results
    • data is name of the data to create the classification model for (i.e., training or holdout data)
stmnl_cm(model, train)
0.5619 = Hit Ratio
0.3413 = PCC
      Level T.Cereal T.Bar T.Oatmeal Total
1  P.Cereal      124    85        46   255
2     P.Bar       52    68         7   127
3 P.Oatmeal       79    21       180   280
4     Total      255   174       233   662
stmnl_cm(model, test)
0.5826 = Hit Ratio
0.3416 = PCC
      Level T.Cereal T.Bar T.Oatmeal Total
1  P.Cereal       45    24        20    89
2     P.Bar       18    25         0    43
3 P.Oatmeal       21     8        57    86
4     Total       84    57        77   218

9.3.3 Average Predicted Probabilities

  • Predicted probabilities can help interpret the effects of the independent variables on the choice dependent variable
  • Use the stmnl_pp user-defined function for each IV to obtain these.
  • Usage: stmnl_pp(model, focal, xlab)
    • model is the name of the object with the saved model results
    • focal is the name of the variable (in quotes) for which predicted probabilities are wanted
    • xlab is optional, but can be provided for a better x-axis label for the plot (e.g., “Income Category”)
  • NOTE 1: For continuous focal variables, the table produced uses three levels to calculate predicted probabilities: \(-1 SD\), \(MEAN\), \(+1 SD\)
  • NOTE 2: This function requires the following packages:
    • tidyr
    • effects
    • dplyr
    • ggplot2
stmnl_pp(model, "age", "Age in Years")
$table
  age   bfast p.prob lower.CI upper.CI
1  31  Cereal 0.5158   0.5727   0.4586
2  31     Bar 0.4134   0.4718   0.3573
3  31 Oatmeal 0.0708   0.1047   0.0473
4  49  Cereal 0.4792   0.5274   0.4314
5  49     Bar 0.2434   0.2874   0.2043
6  49 Oatmeal 0.2773   0.3255   0.2338
7  67  Cereal 0.2657   0.3196   0.2180
8  67     Bar 0.0856   0.1199   0.0604
9  67 Oatmeal 0.6487   0.7035   0.5897

$plot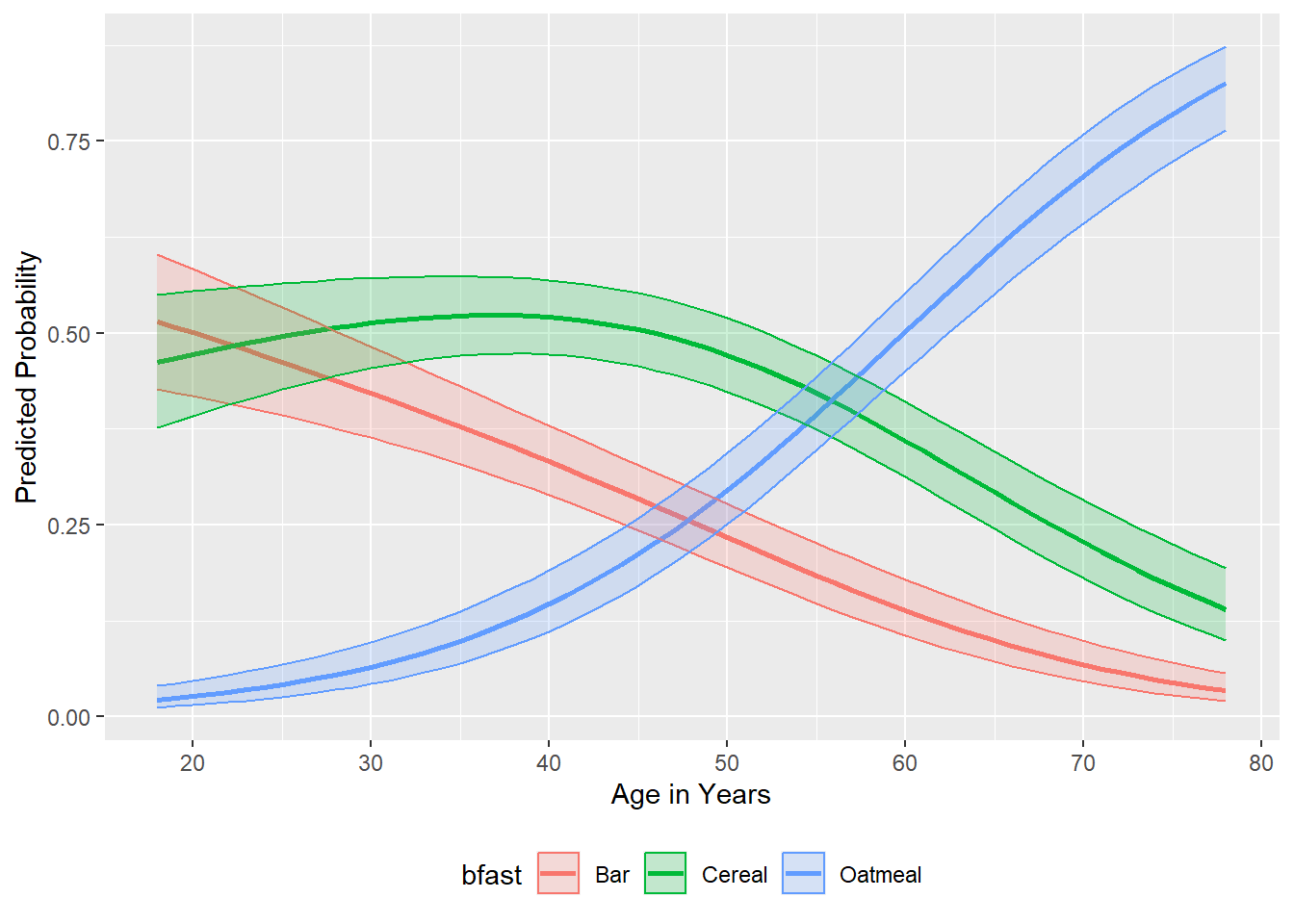

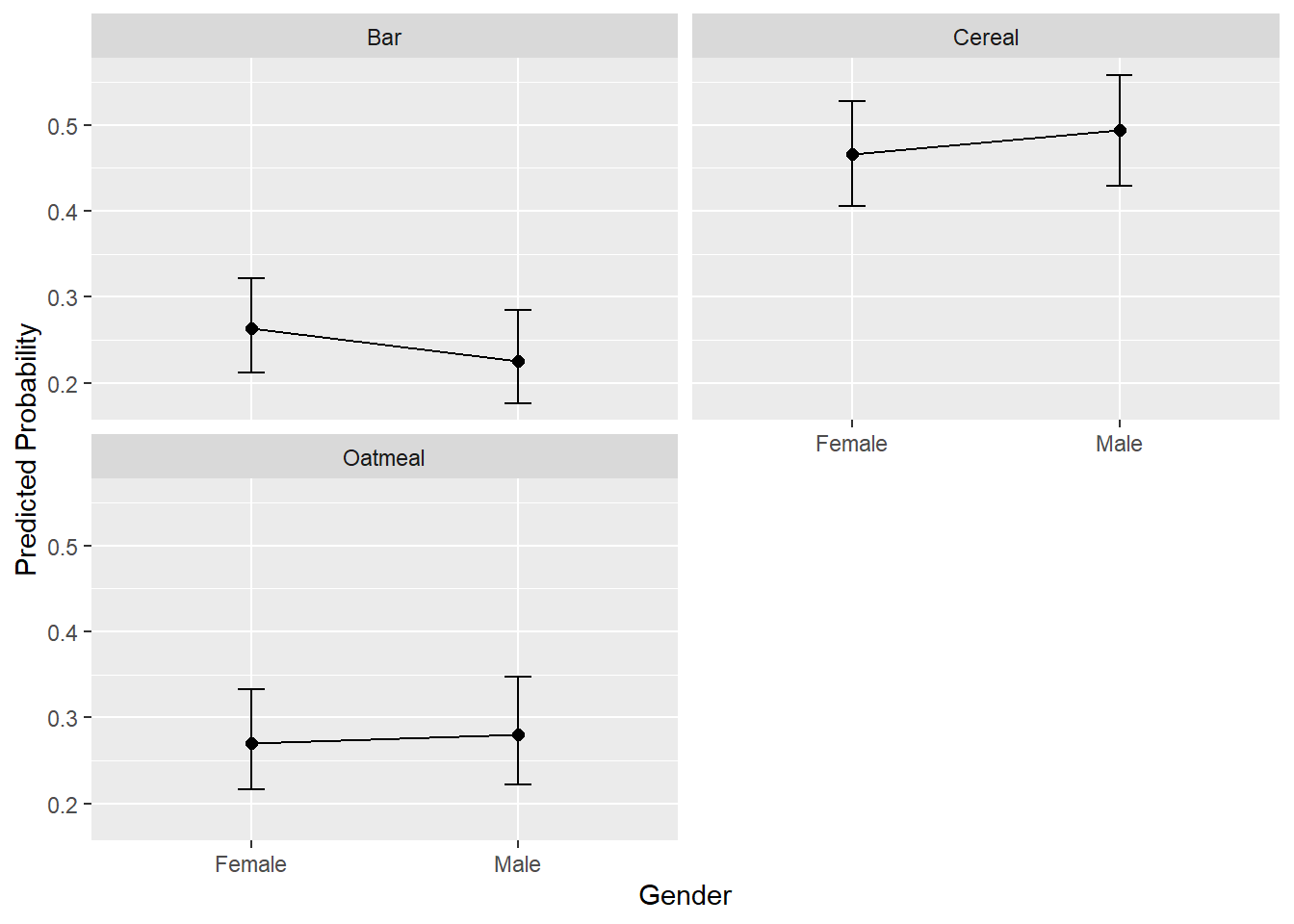
stmnl_pp(model, "gender", "Gender")
$table
  gender   bfast p.prob lower.CI upper.CI
1 Female  Cereal 0.4660   0.5276   0.4053
2 Female     Bar 0.2634   0.3219   0.2122
3 Female Oatmeal 0.2706   0.3324   0.2166
4   Male  Cereal 0.4939   0.5584   0.4296
5   Male     Bar 0.2257   0.2848   0.1758
6   Male Oatmeal 0.2804   0.3473   0.2221

$plot